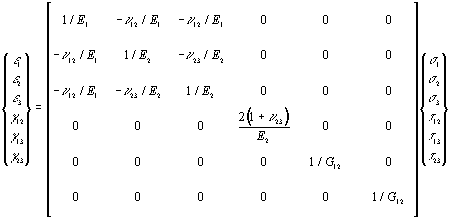Berechnung spritzgegossener kurzfaserverstärkter Kunst-
stoffbauteile unter statischer und thermischer Last

Vortrag auf XXIV. FEM-Kongress in Baden-Baden

am 17./18.November 1997

Gerhard Schmöller

Abstract

Bauteile aus kurzfaserverstärkten Kunststoffen werden in vielen Bereichen der Industrie aufgrund ihrer guten mechanischen und thermischen Eigenschaften und ihrer Eignung zur Großserienfertigung im Spritzgußprozeß in zunehmendem Maße eingesetzt. Wird als Matrixwerkstoff ein Thermoplast eingesetzt, zeichnen sich diese Werkstoffe im Vergleich zu den meisten anderen Verbundwerkstoffen durch ihre gute Recyclingfähigkeit aus.

Während für Faserverbundbauteile aus gerichteten Laminaten seit Jahren brauchbare und verifizierte Berechnungsmethoden sowohl analytischer Art, als auch basierend auf die FEM existieren, stehen die Bemühungen, Methoden zur Vorhersage des mechanischen und thermischen Verhaltens von kurzfaserverstärkten Werkstoffen zu entwickeln, sowie vor allem deren praktische Anwendung noch relativ am Anfang.

Im Folgenden soll einen Überblick über die verschiedenen Rechenansätze auf diesem Gebiet geliefert und die Möglichkeiten aufgezeigt werden, wie Bauteile aus diesen Werkstoffen mit heute verfügbaren CAE-Programmen einer Berechnung zugeführt werden können.

Materialverhalten kurzfaserverstärkter Kunststoffe

Wie bei allen Verbundwerkstoffen ergeben sich auch bei kurzfaserverstärkten Kunststoffen die mechanischen und thermischen Eigenschaften des Verbunds aus dem Zusammenspiel der einzelnen Komponenten, in diesem Fall zwischen Matrix und Faser. Sind die Fasern rein stochastisch und örtlich gleichmäßig verteilt, ergibt sich für das Bauteil ein quasiisotropes Materialverhalten, das relativ einfach sowohl bei der Bestimmung der Werkstoffkennwerte als auch bei der Berechnung handhabbar ist. Ähnliches gilt für gerichtete Laminate mit transversal isotropem Verhalten, für die Werkstoffkennwerte in Faserrichtung und senkrecht dazu ausreichen, um das Verhalten des Verbundes zu kennzeichnen. Im Gegensatz dazu ist für spritzgegossene Bauteile eine durch den Herstellprozeß bedingte örtliche Faserausrichtung und -verteilung kennzeichnend, die eine Vorhersage des örtlichen Materialverhaltens erschwert. Um zu einer für eine FEM Berechnung brauchbaren Materialbeschreibung dieser Werkstoffe zu gelangen sind also folgende zwei Problemkreise zu lösen:

• Bestimmung der örtlichen Faserorientierung und Verteilung
• Bestimmung der sich hieraus ergebenden Materialkennwerte

Bestimmung der Faserorientierung und –verteilung

Das Hauptproblem bei der Berechnung von kurzfaserverstärkten Werkstoffen lag hierbei in der Vergangenheit sicher bei der Bestimmung der örtlichen Faserorientierung und –verteilung. Es wurden zahlreiche Versuche unternommen, die Faserorientierung experimentell mit teilweise sehr aufwendigen Methoden (z.B. Röntgen, mikroskopische Auswertung von Schliffbildern, ...) zu bestimmen. Liegen auf diese Weise ermittelte Werte vor, stellt ihre Aufbereitung in ein für Berechnungen brauchbares Format immer noch ein großes Problem dar.

Seit einigen Jahren sind jedoch zur Auslegung spritzgegossener Bauteile sogenannte rheologische Berechnungsprogramme auf Basis der FEM verfügbar, die hauptsächlich zur Bestimmung optimaler Prozeßparameter (Fülldruck, Temperaturführung...) bei der Herstellung, sowie zur Voraussage von Verzug, Schwindung und Lage der Bindenähte eingesetzt werden. Einige dieser Programme erlauben darüber hinaus auch die Berechnung der Faserorientierung und des Orientierungsgrades bei verstärkten Füllmassen.

Diese Programme verwenden in der Regel dreiecksförmige Schalenelemente mit mehreren Schichten (Layern) über die Dicke. Damit können unterschiedliche Faserausrichtungen über die Dicke des Bauteils berücksichtigt werden (Abb. 1). Entsprechende Elemente sind auch in den meisten “klassischen” FEM Programmen verfügbar und werden dort z.B. zur Berechnung von Laminaten oder anderen Werkstoffen mit schichtweisem Aufbau eingesetzt.

Damit ist prinzipiell eine direkte Übertragung der von den rheologischen Programmen berechneten Orientierungsergebnisse zu allgemeinen FEM Programmen für weitergehende Berechnungen möglich.

Abb. 1: schichtweiser Shellaufbau mit unterschiedlicher Materialorientierung in den einzelnen Layern

Beschreibung des nicht isotropen Werkstoffverhaltens faserverstärkter Werkstoffe

Zur Behandlung des zweiten Problemkreises der Werkstoffkennwerte in Abhängigkeit von der lokalen Faserorientierung und –verteilung soll nun kurz auf die Grundlagen der Beschreibung nicht isotroper Werkstoffe eingegangen werden.

Abb.2: Werkstoffkennwerte in Abhängigkeit von der Faserorientierung

Das mechanische Verhalten eines Werkstoffes wird durch die Spannungs-Dehnungs-Beziehung beschrieben. Im einfachsten Fall einer einachsigen Belastung bei linear elastischem isotropem Materialverhalten lautet dieser Zusammenhang z.B. bei Zug in einer Richtung. Im allgemeinen räumlichen Fall und unabhängig vom zugrunde gelegten Materialgesetz (elastisch, elastisch-plastisch, viskoelastisch, usw.) läßt er sich durch den Vektor der Dehnungen, der sog. konstitutiven Matrix und dem Vektor der resultierenden Spannungen darstellen.

Im Gegensatz zu isotropen Werkstoffen, bei denen das Materialverhalten unabhängig von der Richtung des Kraftangriffs ist, wird sich bei orthotropen oder anisotropen Werkstoffen je nach Richtung des Kraftangriffs eine andere Dehnungsantwort einstellen.

Für kurzfaserverstärkte Kunststoffe kann bei infinitesimaler Betrachtungsweise transversal isotropes Verhalten als Sonderfall der Orthotropie angenommen werden. Davon spricht man, falls für jeden Punkt im Material eine Ebene der Isotropie existiert. Dies kann gut an einem einzelnen Faser-Matrix-Element dargestellt werden:

In der Ebene senkrecht zur Faser ist das Materialverhalten unabhängig von der Richtung. D.h. das Spannungs-Dehnungs-Verhalten z.B. bei Zug in 2-Richtung wird sich nicht vom Verhalten bei Zug in (hier nicht dargestellter) 3-Richtung unterscheiden. Das Material verhält sich in dieser Ebene also isotrop (Abb. 2). Deshalb werden in diesem Fall lediglich 5 unabhängige Materialkonstanten benötigt (Im Gegensatz zu orthotropem Material mit 9 und anisotropem mit 21 unabhängigen Konstanten).

Die Spannungs-Dehnungs-Beziehung für linear elastisches transversal isotropes Material hat daher folgende Form:

Die Bestimmung der Ingenieurkonstanten E₁, E_2,, n₁₂, n₂₃ und G₁₂ kann nun entweder experimentell oder aufgrund theoretischer Überlegung erfolgen.

Mikromechanische Ansätze zur Beschreibung faserverstärkter Kunststoffe

Die theoretische Vorgehensweise wird durch sogenannte mikromechanische Ansätze abgedeckt. Sie dienen dazu, das mechanische und thermische Materialverhalten von Verbundwerkstoffen aus den Werten der einzelnen (isotropen) Komponenten (Faser und Matrix) zu bestimmen. Dies reduziert den nötigen meßtechnischen Aufwand erheblich, da keine richtungsabhängigen Messungen vorgenommen werden müssen. Ebenso können Änderungen bei Faserlänge oder -durchmesser, sowie im Faseranteil leicht berücksichtigt werden

Mechanisches Verhalten

Für das mechanische Verhalten findet meist der Ansatz nach Halpin und Tsai /6/ Verwendung ( l Faserlänge, d Faserdurchmesser, V_f Faservolumenanteil, Index M: Matrix und Index F: Faser):

	mit		und
	mit		und
	mit		und

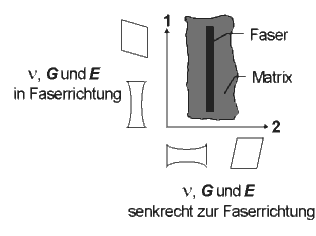
Der Schubmodul in der 2-3-Ebene kann nach Halpin und Kardos /6/ berechnet werden:

Die Querkontraktionszahl bei Zug in Faserrichtung wird allgemein nach der Mischungsregel ermittelt /6/:

Andere Theorien zu mikromechanischen Verhalten von Verbundwerkstoffen wurden z. B. von Tandon & Weng /10/, und Cox /8/ veröffentlicht.

Thermisches Verhalten

Als Beispiel für entsprechende Ansätze zur Berechnung der unterschiedlichen thermischen Ausdehnung sei hier der Ansatz nach Marom & Weinberg /5/ dargestellt:

Bei unidirektionaler Faserorientierung gilt für den Ausdehnungskoeffizienten in Faserrichtung

und für den Ausdehnungskoeffizienten quer zur Faserrichtung

Der Faktor k (0 < k <1) dient wie die Halpin-Tsai-Parameter x_i zur Anpassung an Meßergebnisse.

Andere Ansätze liegen von Cox /8/, Scharpery /4/und Schneider /9/vor.

Verwendung experimentell bestimmter Materialkennwerte

Die Messung von mechanischen und thermischen Materialkennwerten von kurzfaserverstärkten Kunststoffen in Abhängigkeit von der Faserverteilung, -orientierung, dem Faservolumenanteil sowie der Temperatur ist sehr aufwendig. Das Hauptproblem stellt hierbei die Herstellung von Proben mit einer möglichst hohen Faserausrichtung dar. Durch geeignete Herstellbedingungen können zwar hohe Orientierungsgrade in der Kernschicht erreicht werden, die nahezu orthogonale Orientierung in den Randschichten im Vergleich zur Kernschicht läßt sich jedoch kaum verhindern. Abhilfe schafft hier nur eine aufwendige mechanische Abtragung der Randschichten. Zur Bestimmung der Materialkennwerte in Abhängigkeit von der Orientierung werden die Proben meist aus Platten mit hoher Orientierung entnommen und zwar in Vorzugsrichtung und senkrecht dazu. Man erhält auf diese Weise einen Satz von Kennwerten, die denjenigen nach den mikromechanischen Theorien entsprechen.

Übertragung auf nicht unidirektionale Faserverteilung

Die oben genannten mikromechanischen Modelle gehen meist von einer unidirektionalen Faserverteilung aus. Auch Meßwerte liegen in der Regel nur für diesen Fall vor. In der Realität treten jedoch Faserverteilungen auf, die sich zwischen diesen beiden Extremen bewegen.

Mit sogenannten makromechanischen Ansätzen wird daher versucht, die Ergebnisse des unidirektionalen Falls auf andere Orientierungsgrade umzurechnen.

Ist neben dem Winkel der Hauptfaserorientierung der prozentuale Anteil von Fasern in dieser Richtung und senkrecht dazu bekannt, kann eine relativ grobe Abschätzung der sich ergebenden Verbundkennwerte nach einer Art Mischungsregel erfolgen:

FOR₁ und FOR₂ sind die prozentualen Anteile der Fasern in der jeweiligen Richtung.

Entsprechend kann bei den anderen thermischen und mechanischen Kennwerten vorgegangen werden.

FEM-Berechnung

Ausgehend von der berechneten Faserorientierung und -verteilung kann nun über die oben genannten mikro- und makromechanischen Ansätze für jedes Element ein Satz orthotroper Materialkennwerte berechnet werden.

Damit stehen theoretisch alle nötigen Kennwerte für statische und thermische FE- Berechnungen (Materialorientierung, mechanische und thermische Kennwerte in Materialrichtung und senkrecht dazu) zur Verfügung.

In der Praxis bereiten allerdings noch einige Punkte Schwierigkeiten:

• kommerzielle Schnittstellen zur Übernahme der Orientierungsdaten und Berechnung der daraus resultierenden Materialkennwerte in gängige FEM Programme sind nicht verfügbar. Dies bedingt eine Eigenentwicklung für das jeweils vorhandene Softwareumfeld.

• lineare Dreiecksschalenelemente sind zwar für thermische Berechnungen gut geeignet, bei statischen Berechnungen aber nicht erste Wahl.

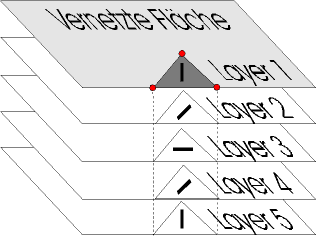
• Durch die Zuweisung eines Materials und einer Orientierung für jedes Element und jede Lage dieses Elements fällt eine große Datenmenge an.

• Beschränkung auf Schalenelemente bei vielen statischen Problemen unzureichend.

Die praktische Umsetzung und Zusammenführung der dargestellten Methodik sei im folgenden am Beispiel einer einfachen Platte (150 x 200 x 5 mm) erläutert:

1. Erstellung eines FE Netzes aus lineraren Dreieckselementen mit einem geeigneten Preprozessor

2. Export des Netzes zum rheologischen Berechnungsprogramm

3. Hinzufügen der für diese Berechnungen zusätzlich erforderlichen Elemente (Angüsse, etc.)

4. Berechnung der Faserorientierung sowie des Ausrichtungsrades. Abb. 3 zeigt die sich einstellende Faserausrichtung in der Mittelschicht des Bauteils. Der dazugehörige Ausrichtungsgrad der Fasern wird durch die Ellipsen symbolisiert. Eine schmale Ellipse steht hierbei für einen hohen Ausrichtungsgrad, während ein Kreis für eine nahezu willkürliche Verteilung steht.

   

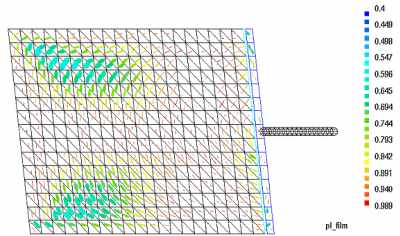
   Abb.3:Faserorientierung und Verteilung in der Mittelschicht

1. Entfernen der zusätzlich modellierten Elemente

2. Berechnung der sich aus dem Ausrichtungsgrad ergebenden Materialkennwerte für jedes Element und jede Lage

3. Übersetzung dieser Daten in ein Eingabeformat für ein strukturelles FEM Programm.

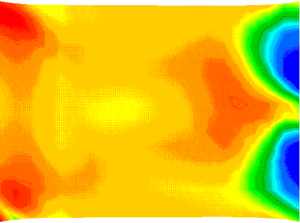
4. Definition der Randbedingungen und Lasten und Durchführung der Berechnung. Die in Abb. 4 und Abb. 5 abgebildeten Ergebnisse stammen von Berechnungen, die ohne Mittelung mit 9 Schichten durchgeführt wurden. Um den Einfluß der Faserverteilung als Folge unterschiedlicher Herstellbedingungen darzustellen, wurde die Platte zusätzlich zum oben dargestellten Filmanguß ebenfalls unter Verwendung eines Punktangusses in der Mitte der Platte berechnet. Die sich ergebenden Materialorientierungen sind in für beide Fälle jeweils in der Mitte der Platte und in der Randschicht dargestellt (Abb. 4). Abb. 5 zeigt qualitativ die sich einstellenden Spannungsverteilungen nach von Mises in den Randschichten der beiden Platten bei einer Zugbelastung und macht deutlich, welchen Einfluß die Faserorientierung auf das Bauteilverhalten hat.

Filmanguß	Punktanguß

Mittelschicht

Randschicht

Abb.4:Materialorientierung in Abhängigkeit von der Herstellung

Filmanguß	Punktanguß

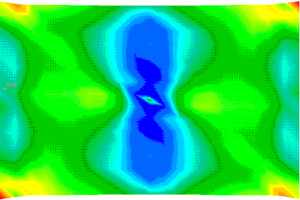Abb.5: Platte unter Zug (Spannungsverteilung nach von Mises in der Randschicht)

Eine weitere Verfeinerung der oben dargestellten Vorgehensweise stellen folgende Schritte dar:

• Übergang auf parabolische oder höherwertige Dreieckselemente oder Vernetzung mit Viereckselementen, nachfolgende Teilung der Viereckselemente in zwei Dreieckselemente für rheologische Berechnung, die danach für die statische Berechnung wieder zu Viereckselementen zusammengefaßt werden.
• Durch die Beschränkung der Materialkennwerte in eine bestimmte Anzahl von Klassen in Abhängigkeit vom Orientierungsgrad kann eine wesentliche Reduzierung der anfallenden Datenmenge erreicht werden.
• Eine Möglichkeit zur Reduzierung des nötigen Rechenaufwands stellt eine Mittelung der Materialorientierungen und –kennwerte über die Dicke dar. Hierbei sind aber folgende Überlegungen zu beachten: Durch den symmetrischen Aufbau der Schichten ist es für statische Berechnungen mit reiner in-plane Belastung sowie bei der Berechnung thermischer Eigenspannungen bei symmetrischer oder konstanter Temperaturverteilung über die Dicke zulässig, die sich ergebenden Materialkennwerte und -orientierungen über die Dicke zu mitteln. Für diese Mittelung muß eine Koordinatentransformation der Materialkennwerte auf die sich ergebende Durchschnittsorientierung durchgeführt werden ( siehe auch Orientation Averaging nach Advani & Tucker /7/). Eine Aussage über den Spannungszustand über die Dicke ist auf diese Art natürlich nicht mehr möglich. In Fällen, in denen Biegebelastung auftritt, entsteht hierbei ein Fehler, da die Materialeigenschaften in der Randschicht durch ihren größeren Abstand zur neutralen Faser das Verhalten des Bauteils unter dieser Belastung stärker beeinflussen als Schichten in der Mitte. Ein noch größerer Fehler tritt auf, falls ein Temperaturgradient über die Dicke existiert, da in diesem Fall auch die Symmetrie der Materialeigenschaften nicht mehr vorhanden ist.
• Übertragung der Ergebnisse für die Schalenelemente auf quaderförmige Volumenelemente mit schichtweisem Aufbau an Stellen, wo auf eine Volumenmodellierung nicht verzichtet werden soll oder kann.
• Übernahme von Schwindung und Verzug, sowie der eingefrorenen Spannungen aus dem Herstellprozeß als Ausgangspunkt für die strukturelle Berechnung
• Verwendung von Materialgesetzen, die das Verhalten von Kunststoffen (Relaxation, Viskoelastizität...) besser beschreiben, als lineare Elastizität

Fazit

Durch die Möglichkeit, die Faserorientierung und -verteilung spritzgegossener kurzfaserverstärkter Bauteile mit rheologischen Berechnungsprogrammen zu bestimmen, ist die Grundlage vorhanden, um auch Bauteile aus diesen Werkstoffen ohne zu große Vereinfachung sowohl unter statischer als auch unter thermischer Last mit gängigen FEM Programmen zu berechnen. Es ergibt sich hierdurch ein geschlossener rechnerischer Ansatz in einem zum Großteil schon verfügbaren CAE Umfeld. Lediglich die Verfügbarkeit kommerzieller Schnittstellen steht hier der praktischen Anwendung noch entgegen. Die Verwendung mikromechanischer Rechenansätze verringert die Anzahl der benötigten Kennwerte drastisch und erlaubt, daß auch Änderungen z.B. beim Faseranteil oder der Faserlänge recht schnell in ihren Auswirkungen simuliert werden können.

Literatur