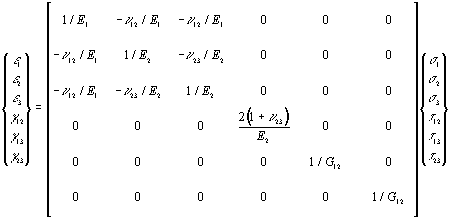Simulation of short fiber reinforced injection molded parts with static or thermal loading

XXIV. FEM-Kongress Baden-Baden, Germany

17./18.November 1997

Gerhard Schmöller

Abstract

Parts made of short fiber reinforced plastics are widely used in different industries according to their good mechanical and thermal properties and their suitability for high volume production based on injection molding. As a further plus, when using a thermoplastic matrix they are better recyclable than other composite materials.

While there are usable and tested methods (both analytical and based on FEM) for laminates, efforts to predict the mechanical and thermal behavior of parts made of short fiber materials are still in the beginning, which is mainly due to a lack of available commercial software offering this possibility.

Below, a survey of existing theories and methods concerning this field will be given and possibilities will be shown to implement these methods in todays CAE applications.

Material behavior of short fiber reinforced plastics

As it is true for all composit materials the mechanic and thermal behavior of the compound is a result of the interaction between the single components, in this case betweeen fiber and matrix. Assuming a random orientation and homogeneous distribution the resulting quasiisotropic behavior is easily handeld concernig both simulation and testing. Similar is true for aligned laminats with transversal isotropic behavior, where the fiberorientation is known and a set of material data parallel and perpendicular the fiberorientation will be enough to describe the behavior of the part.

In contrast to this, the fiber orientation and distribution in parts made of SFRTs is highly dependent on the molding process and therefore nearly impossible to predict.

To come to a material description usable in FEA, the following problems have to be solved:

• determination of the local fiberorientation and distribution
• determination of the resulting material behavior

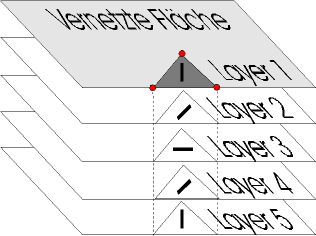
Determination of Fiberorientation and -distribution

In the past, the main problem concerning the calculation of short fiber reinforced parts certainly was the determination of the local fiberorientation and distribution. Many experimental attempts were made to meassure these quantities (e.g. using X-Ray or image analysis on cutting planes). Beside of the costs of these methods - and ignoring the fact that there has to be a real part, which is contradictory to the aim of most simulations-, converting the results to CAE formats still remains a problem.

Since a couple of years however rheological programs such as Moldflow™ and C-Mold™ are available, which are mostly used to optimize the molding process. Some of these systems in addition allow the calculation of fiber orientation and distribution. These kind of programs mostly use triangular shells with several layers across thickness. This way it is possible to take into account the different fiber orientation across the thickness. Corresponding elements are available for most classical FEM solvers, making a direct transformation of results possible.

Fig. 1: layered shells with different material orientations

Nonisotropic behavior of fiber reinforced materials

Comming to the second field of problems, a short recapitulation of the basics of non isotropic materials may be helpful.

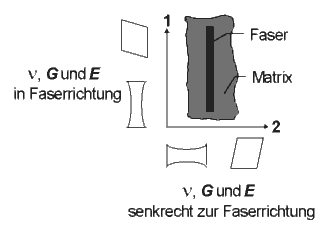
Fig.2:engineering constants dependent on fiberorientation

A materials mechanical behavior can be specified using the stress strain relationship. In the most simpel case of linear elastic, isotropic material with single axis loading this relationship reduces to .

To describe the most general case in space, independent of the material law one needs the strain vector, the so called constitutive matrix and the stress vector.

In contrast to isotopic materials where the material behavior is independent from the direction of the applied force, the strain answer will vary with direction using orthotropic or anisotropic materials.

Viewing at a single fiber-matrix-cell the behavior can be regarded to be transversal isotropic as a special case of orthotropic behavior. This is the case if there is a isotropic plane for each material point in the part.

In the plane perpendicular to the fiber, the material behavior is direction-independent. That is, the stress-strain-behavior with tension in the 2-direction will be equal to that in 3-direction (not shown here). Thus the material in the 2-3-plane is isotropic (Fig. 2). Therefore only five independent material constants are needed to describe the material behavior (orthotropic matererials need 9 and anisotropic 21).

The stress-strain-relationship for linear elastic, tranversal isotopic materials may be therefore given in the following manner:

The determination of the engineering constants E₁, E_2,, n₁₂, n₂₃ und G₁₂ may now be done using experimental data or following theoretical considerations.

Micromechanical description of fiber reinforced plastics

The theoretical way follows so called micromechanical approaches which try to predict the mechanical and thermal behavior of the compound using the (isotropic) data of the composits fiber and matrix and thus reducing the testing costs, because direction dependent experiments are not needed. In addition, changes in fiber length and diameter, as well as in fiber fraction can be easily considered.

Mechanical Behavior

Looking at the mechanical behavior the approach from Halpin und Tsai /6/ is commonly used ( l fiberlength, d fiberdiameter, V_f fibervolumefraction, index M: matrix and index F: fiber):

The shear modulus within the 2-3-plane may be obtained following Halpin and Kardos /6/:

Poisson's ratio is commonly determined by a rule of mixture /6/:

There are other theories concerning micromechanics of composits, giving Tandon & Weng /10/ and Cox /8/ as an example.

Thermal Behavior

As an example for calculating the thermal expansion coeffizients in a corresponding manner, the approach of Marom & Weinberg /5/ will be explained here:

Assuming unidirectional fiberorientation the thermal expansion coefficient parallel fiber is

and for that perpendicular fiber they give

The factor

(0 <

<1) serves like the Halpin-Tsai-parameters

for fitting with experimental data.

Other approaches are known from Cox /8/, Scharpery /4/and Schneider /9/.

Use of experimental Data

Meassurement of mechanical and thermal material properties of fiber reinforced materials depending on fiber distribution, orientation and volume fraction as well as temperature is very expensive. One main problem is the production of specimens with sufficiently alligned fibers. Suitable production may assure high grades of fiber orientations in the central layer, but the nearly orthogonal orientation in the boundary layers is hardly to avoid. To find a remedy costly mechanical removing of the boundary layers is needed.

To determine the material constants in dependency on orientation the specimen are taken from plates with high orientation in the main direction and perpendicular. Thus a set of values is obtained which corresponds to that calculated with micromechanical approaches.

Transfer to non unidirectional Fiber Orientation

The discussed micromechanical approaches mostly suppose unidirectional fiber alignment. Meassured values also are given this way. In reality allignment of the fibers will exist between these extremes.

So called macromechanical approaches are used to transfer the results from the unidirectional case to different fiber alignments.

Given the angle of the main fiber orientation and the percentage of fibers aligned in this direction and perpendicular, a kind of rule of mixture may be used to achive an estimate of the resulting composite behavior:

FOR₁ und FOR₂ are the percentage of fibers in the respective direction.

The other thermal an mechanical values are obtained accordingly.

FE simulation

Based on the calculated fiber orientation an distribution and using the delivered micro and macromechanic methods a consistent set of orthotropic values can be obtained for each element.

Thus, all needed material data needed for static and thermal analyses (material orientation, thermal and mechanical properties parallel and perpendicular to fiber direction) are available.

In practice some points still cause difficulties:

• there are no commercial interfaces available on the market which allow transfering of orientation data and calculating the resulting material data to common FEA systems
• linear triangular elementes are well suited for thermal calculations, but cause well known problems when used for structural analyses
• giving each element and each element layer individual material and orientation values causes a huge amount of input data

The following example with a simple plate (150 x 200 x 5 mm) shows the proceeding when combining the above:

1. triangular meshing using an arbitary preprocessor
2. mesh export to the rheologic program
3. adding of specific Elements and boundary conditions (runners, ...)
4. calculation of fiber orientation and alignment. Fig. 3 shows the predicted orientation in the central layer. The respective alignment is represented by ellipses. A slim ellipse stands for high alignment, whereas a circle means random distribution.



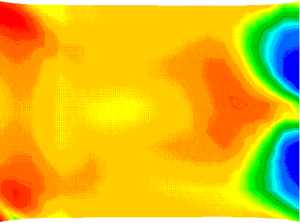
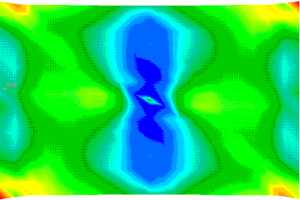
Fig.3:Fiberorientation and distribution (central layer)

1. removal of additional elements
2. calculation of material constants for each element and each layer based on fiber alignement
3. translation of these data to the input format of the used structural FEA solver
4. definition of boundary conditions and loads and running the simulation. The results shown in Fig. 4 and Fig. 5 are obtained from simulations without averaging and 9 layers. To show the influence of different molding conditions, the plate was in addition to the shown fan gate calculated with a point gate in the center of the plate. The resulting Materialorientations are shown at each cases for the central and boundary layer (fig. 4). Fig. 5 shows the significant differences of the von mises stress distribution under tension in the boundary layers of both cases.

Fan gate	Needlegate

central layer

boundary layer

Fig.4:materialorientation with respect to production

fan gate	Punktanguß

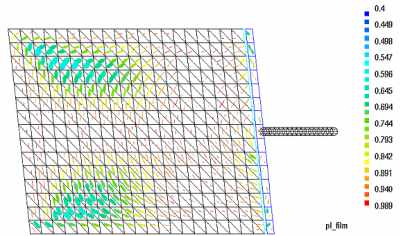
Fig.5:Plate under tension (von Mises stresses in the boundary layer)

Further improvements may be achieved according to the following steps:

• Using parabolic or higher order triangular elements or meshing with quadrilateral elements followed by splitting these quads in two trias for the rheologic simulation and rejoining afterwards for the structural analyses.
• classification of materials based on ranges of fiber alignement may achive a significant reduction of data.
• to further reduce the simulation costs and amount of data one could average the orientations and materials across the shell thickness. Doing so, some points have to be taken into account: due to the symmetrical setup of the layers assuming pure in plane loads or constant temperature distribution such averaging is allowed. To build the average, a coordinate tranformation of the material properties to the main orientation has to be performed (see Advani & Tucker /7/ : Orientation Averaging). A statement about the stress state across thickness obviously is not possible any more. Cases where bending is involved are not suitable for orientation averaging, because the material properties in the boundary layer take much more influence on the bending behavior than those in the center, due to their greater distance to the neutral fiber. Evern greate errors occure, if there is a temperature gradient accross the thickness, as in this case not even the symmetry of the material properties remains.
• taking over of shrinkage and warp, as well as residual stresses as starting point of the structural FEA

• Making use of material laws better matching the behavior of plastics (relaxation, viscoelasticity...) than linear elasticity

Conclusion

Given the possibility of calculating fiber orientation and distribution of molded short fiber reinforced parts with rheolocic software the prerequisites are met for thermomechanical simulations with parts made of these materials without to much simpilification with common FEA solvers. Thus, a closed solution within existing CAE environments is possible. Solely the lack of commercial interfaces still prevents all day use. Micromechanical approaches reduce the number of needed material constants and even allow the prediction of changes in the parts behavior caused by changes in fiber volume fraction or fiber length.

Literature